До самого последнего времени ходили слухи, что в 2012 году Нобелевский комитет отметит исследования долговых и банковских кризисов - тем, как никогда актуальных в последние годы. Но комитет поступил консервативно: нобелевская премия в области экономики досталась Ллойду Шепли за теорию 50-летней давности и Элвину Роту - за ее приложение на практике.
Немного теории
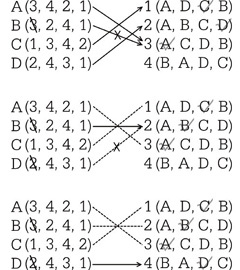
Схема выбора в рамках алгоритма Гейла-Шепли
(Нажмите чтобы увеличить)
Lenta.ru
В 1962 году в журнале American Mathematical Monthly появилась работа "Поступление в колледж и стабильность браков" (College admissions and the stability of marriage) математиков Девида Гейла (он не дождался премии и скончался в 2008 году) и Ллойда Шепли из Университета Брауна и Принстонского университета, соответственно. В этой работе, которая относилась к теории так называемых коалиционных игр, ученые рассматривали следующую формальную задачу, получившую позже название задачи о марьяже.
Условия таковы. Пусть даны два множества M и Ж, причем для каждого элемента из М элементы из Ж отсортированы в некотором порядке. То есть мы можем говорить, какие элементы Ж для данного элемента m из М являются более предпочтительными, а какие менее. Сортировки, конечно же, для каждого элемента могут быть свои. Аналогичные предпочтения введены и для элементов из Ж. Суть задачи сводится к разбиению M и Ж на пары. В каждую пару берется по одному элементу из M и из Ж. При этом в результате мы должны получить не просто разбиение, а так называемое стабильное разбиение. Стабильность - общее понятие для теории игры, которое в данном конкретном случае означает, что отсутствуют пары (m, ж) и (m', ж'), обладающие таким свойством: для m элемент ж' является предпочтительнее ж, а для ж' элемент m является предпочтительнее m'.
Если такая формулировка кажется читателю занудной, то у этой задачи есть весьма наглядная интерпретация, кстати, объясняющая название "задача о марьяже". Представим себе, что М и Ж - это множества мужчин и женщин, которые, по причинам возраста или каким иным, очень хотят вступить в законный брак. Решающий задачу в этом случае выступает в роли свахи - его цель переженить всех потенциальных женихов и невест так, чтобы полученная система браков была стабильной. В такой интерпретации стабильность означает, что среди наших молодых семей не будет таких, чтобы мужа из одной семьи и жену из другой тянуло друг к другу сильнее, чем к своим законным половинкам (ведь наличие подобной тяги вполне могло бы стать причиной для развода).
По данным агентства Thomson Reuters, нобелевскими лауреатами 2012 года должны были стать Энтони Аткинсон, Ангус Дитон, Стивен Росс или Роберт Шиллер. Первый занимается изучением неравенства доходов; второй - исследованиями потребления, доходов, сбережения, бедности; третий - теорией ценообразования; четвертый - волатильностью финансовых рынков.
Шиллер назывался в числе фаворитов и российским экономистом Константином Сониным, который дает нобелевские предсказания каждый год. Сонин же отметил, что в этом году в сентябре был проведен так называемый нобелевский симпозиум. Он был посвящено росту и развитию, поэтому экономисты предполагали, что именно в этой отрасли и следует искать нового нобелевского лауреата. На самом симпозиуме выступали уже упоминавшийся Ангус Дитон и еще два десятка экономических звезд первой величины, но нобелевский комитет решил никому из них премии не давать. В годы проведения нобелевских симпозиумов по экономике (их было всего шесть) - это второй такого рода случай, в основном премии присуждаются именно по теме симпозиумов.
Тут, кстати, уместно заметить, что стабильность вовсе не означает, что все семьи будут счастливы - то есть вполне могут быть мужья, которых тянет к чужим женам сильнее, чем к своим, и viсе versa. Более того, может оказаться, что все молодожены несчастливы: рассмотрим трех мужчин M1, M2, M3 и трех женщин Ж1, Ж2, Ж3. Представим, что для первого мужчины список женщин, отсортированных в порядке возрастания желанности выглядит как {Ж3, Ж1, Ж2}, для второго - {Ж1, Ж2, Ж3}, и для третьего - {Ж2, Ж3, Ж1}. В свою очередь, аналогичные списки для женщин выглядят следующим образом: {М3, М1, M2} для первой, {M1, M2, M3} для второй и {M2, M3, M1} для третьей. В этом случае легко проверяется, что система браков (M1, Ж1), (M2, Ж2) и (M3, Ж3) устойчива, но при этом ни один из супругов не счастлив - все жаждут кого-то другого. Впрочем, в теории игр устойчивость оказывается гораздо важнее счастья отдельных участников.
Гейлу и Шепли удалось придумать алгоритм для решения задачи о марьяже. Работает он следующим образом. Пусть начинают мужчины. На первом шаге каждый жених идет к лучшей кандидатке. Если к одной даме посваталось несколько женихов, то из обладателей предложенных ей рук и сердец она выбирает самого милого ей, но, следуя женской натуре, не соглашается, а говорит "Может быть". Всем остальным же она дает от ворот поворот, и расстроенные женихи вычеркивают гордячку из своих списков. На следующем шаге каждый из женихов снова идет к самой желанной (из оставшихся) в своем списке, и ситуация повторяется. После некоторого количества свиданий все мужчины и женщины оказываются разбиты на пары.
Процесс заведомо конечен - отвергнутые мужчины каждый раз делают предложение новым женщинам, а их конечное число. Почему в результате получается стабильная конфигурация? Рассмотрим две пары (m, ж) и (m', ж'), в которых мужа m тянет к жене ж' сильнее, чем к своей. Но это означает, по построению, что в какой-то момент m делал предложение ж' - она была в списке выше его теперешней жены - и был отвергнут. То есть уже на тот момент среди ухажеров ж' был тот, который нравится ей больше m. Учитывая, что женщины меняют женихов только тогда, когда появляется партнер, привлекательнее предыдущего, получаем, что эту жену уж точно не тянет к m сильнее, чем к собственному мужу.
Сложность полученного алгоритма приемлема - для вычисления оптимальной конфигурации требуется порядка n2 операций, где n - число мужчин и женщин. Кстати, уместно заметить, что начинающая сторона алгоритма Гейла-Шепли всегда оказывается в более выигрышной (в некотором смысле) позиции. Грубо говоря, мужчины, берущие инициативу в свои руки, находят себе более подходящих жен, чем пассивные мямли.
У задачи о марьяже существует несколько обобщений. Самое простое - это неравное число партнеров, однако, оказывается, алгоритм Гейла-Шепли там эффективно работает. Есть еще, например, задача о выборе колледжа (она фигурировала в названии оригинальной работы). В этом случае вместо мужчин фигурируют студенты, а вместо женщин - учебные заведения. От основной задачи эта отличается тем, что учебные заведения могут принимать более одного студента. Эту же задачу можно интерпретировать как задачу о марьяже с разрешенной полиандрией - формой полигамии, в которой женщина состоит в браке с несколькими мужчинами. Для этого случая есть аналог алгоритма Гейла-Шепли. Наконец, существует задача о соседях по комнате. В ней вместо двух множеств - мужчин и женщин - есть одно множество. Это эквивалентно разрешению в задаче о марьяже гомосексуальных пар. В этом случае стабильных конфигураций может и не быть. Например, если у нас есть два мужчины M1 и M2 и женщина Ж1, и при этом M1 больше любит Ж1, Ж1 - M2, а M2 - M1. Разного рода обобщения (например, задача о гаремах) можно посмотреть тут и тут (осторожно, pdf!).
codebase="http://fpdownload.macromedia.com/get/flashplayer/current/swflash.cab"> width="800" height="600" name="smp" align="middle"
play="true"
loop="false"
quality="high"
type="application/x-shockwave-flash"
pluginspage="http://www.adobe.com/go/getflashplayer">
Практическое применение
В 80-х годах прошлого века экономист Элвин Рот, тогда сотрудник Университета в Питтсбурге, заинтересовался успехом программы NRMP (National Resident Matching Program - Национальной программы по распределению ординаторов). Дело в том, что в 40-х годах в США наметился дефицит докторов. По этой причине больницы принялись конкурировать за студентов медицинских университетов. Это привело к тому, что позицию ординатора стали предлагать будущим докторам уже тогда, когда они еще толком не выбрали специализацию. Вследствие этого, если студент отказывался от позиции, то место "терялось" - предлагать его кому-нибудь другому было уже слишком поздно. В ответ на это медицинские учреждения ввели строгие временные ограничения, в рамках которых студенты должны были дать ответ о том, принимают ли они предложение или нет.
Это привело к довольно странной ситуации: доктора выбирали больницы в спешке, как и специальности. Это не могло не сказаться на качестве медицинского персонала. Именно поэтому в 50-х годах прошлого века заработала программа NRMP, которая оказалась крайне эффективной. Анализ Рота показал, что в своей работе программа использовала алгоритм, похожий на предложенный Гейлом и Шепли. Более того Рот предположил, что успех программы был обусловлен именно тем, что алгоритм Гейла-Шепли давал стабильные пары.
Впрочем, теория Рота так и осталась бы теорией, если бы в 90-х годах в работе программы не стали возникать перебои. Рост количества студентов-женщин привел к росту числа как официальных, так и неофициальных браков. Не удивительно, что влюбленные пытались попасть в один и тот же госпиталь. Этого алгоритм NRMP не учитывал. В результате руководство программы обратилось к Роту, который в нескольких теоретических работах разработал обобщение алгоритма Гейла-Шепли для этого нового, возникшего на практике случая. В 1997 году NRMP взяла на вооружения модификацию Рота.

Элвин Рот и Ллойд Шепли. Фото (c)AFP
(Нажмите чтобы увеличить)
Lenta.ru
Однако, студенты медвузов оказались не единственными, кому помог алгоритм Гейла-Шепли. В Нью-Йорке выбор учениками школ был организован таким образом: каждый ученик готовил список школ, куда он хотел бы попасть. После этого списки рассылались по школам, которые выбирали кого принять, кому отказать, а кого поместить в список на ожидание. Процесс повторялся еще дважды, и школьники, которые оказывались без школы, размещались административными методами. Со временем, однако, такая система перестала устраивать и школьников, и их родителей, поэтому в 2003 году администрация обратилась за помощью все к тому же Элвину Роту, который обеспечил их собственной версией алгоритма Гейла-Шепли. В 2005 году на аналогичный алгоритм перешел Бостон, а в 2011-м - Денвер и Новый Орлеан.
Насколько хорошо работала получившаяся система? Вот что написал экономист Константин Сонин в своем ЖЖ еще в июле 2012 года по поводу доклада Парага Патака из Массачусетского технологического института. Доклад был посвящен анализу последствий внедрения алгоритмов Гейла-Шепли во всех этих городах:
"Понятно, что это адова, требующая исключительного мастерства эмпирическая работа (впрочем, профессор-географ Михайлова, эмпирик, сидящий рядом, говорит, что профессор Косенок делает такие упражнения шутя) – нужно исключить огромное количество посторонних факторов, которые могут повлиять на результат. Последствия введения новой системы есть, и значимые: более вероятно, что не покидают школу, более вероятно, что не нарушают то, что предписано алгоритмом (при возможности). Плюс сократилось расстояние до школы (само по себе, самой собой, это не означает, что школьникам стало лучше - плохая школа может быть ближе, но это - косвенный показатель того, что результат стал ближе к предпочитаемому). Нет последствий для успеваемости (Бостон и Нью-Йорк - города в нижних 25 процентах по успеваемости в стране). Хорошие новости и для экономики общественного сектора (есть технические решения, улучшающие жизнь людей), и для теории игр."
Еще одной сферой применения модифицированной версии алгоритма Гейла-Шепли стали вопросы трансплантологии. Специально для этого случая была разработана версия алгоритма, в которой вторая сторона (в нашем основном примере - женщины) абсолютно пассивна и не участвует в выборе. Эти наработки, выполненные, кстати, самим Шепли, позволили докторам разрабатывать схемы, в которых, например, почка от донора-родственника идет не больному, а, например, третьему лицу, а уже его родственник дает почку для первоначального больного. Разумеется, количество обменов в таком цикле может быть много больше двух.
Наконец последней из отмеченных Нобелевским комитетом сфер применения алгоритма Гейла-Шепли стали разного рода рынки. В частности, теоретические работы позволили установить, что механизм цены-оплаты вполне можно встроить в алгоритм. Так, подобного рода работы оказались полезны для изучения функционирования интернет-аукционов, в некотором смысле отличных от обычных.
Приведенные примеры, конечно, не исчерпывают весь спектр применения работ Гейла и Шепли (подробнее о том, где еще их труды могут быть полезны, можно прочитать на страничке Элвина Рота). Впрочем уже названных достаточно для того, чтобы ответить на критику, которую в последние годы довольно часто адресуют экономической премии: мол, дают как бы престижную награду за финансовые химеры. В этом году все не так. Награду дали за большое и очень важное дело - теорию, в которой и деньги-то не фигурируют вообще. Только чистая, полезная и очень азартная математика.
