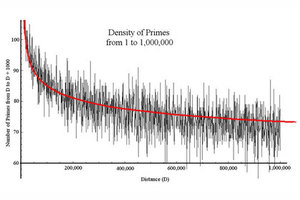
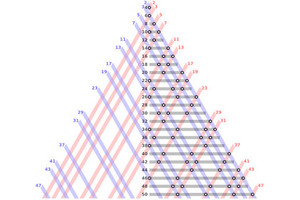
13 ноября 1843 года на заседании Ирландской королевской академии сэр Уильям Роуэн Гамильтон представил свою первую посвященную кватернионам работу On a new Species of Imaginary Quantities connected with a theory of Quaternions (.pdf). В дальнейшем кватернионы постигла печальная судьба — сперва их открытие встретили как божественное откровение, но уже через каких-то сорок лет они вызывали у математиков стойкую идиосинкразию, а еще через сорок лет про них почти никто не вспоминал.
Сами кватернионы, разумеется, в таком развитии событий практически не виноваты. Единственно что можно, пожалуй, поставить им в вину — это то, что, будучи объектом алгебраическим, они выглядели вызывающе геометрично (подробнее об этом чуть ниже). Все остальное — влияние исключительно человеческого фактора.
Математик-невидимка
Начать историю следует не с сэра Уильяма Гамильтона, а с другой, тоже довольно известной личности — банкира-социалиста, близкого ученика Сен-Симона Бенжамена Оленда Родригеса. Сын ростовщика, он в 1815 году закончил Высшую нормальную школу в Париже. Сразу после университета Родригес занялся спекуляциями на бирже — и неплохо в них преуспел.

Бенжамен Олинд Родригес
Спустя всего несколько лет недавний студент был уже директором банка и весьма обеспеченным человеком. В 1823 году Родригес встретил графа Анри Сен-Симона и попал под влияние идей философа-утописта. Влияние было настолько сильным, что Родригес стал одним из самых ярких сторонников Сен-Симона (и, по совместительству, основным спонсором философских изысканий графа).
В 1829 году, уже будучи известным социалистом, успев поучаствовать в издании социалистического журнала Le Producteur, Родригес вышел из руководства движением, которое после смерти самого Сен-Симона плавно, но неотвратимо трансформировалось в секту. Причиной для разрыва, как говорят, стали радикальные взгляды сектантов на отношения между полами. В 1832 Родригес окончательно покинул общину, оставив утопистов практически без денег. До конца жизни (1851 год) банкир продолжал называть себя убежденным социалистом.
Порвав с сенсимонистами, Родригес вдруг вспомнил о математике (а быть может, и просто о беззаботной студенческой юности). Что конкретно послужило тут толчком, достоверно неизвестно. Впрочем, это и не важно; важно лишь то, что в 1840 году Родригес опубликовал в далеко не последнем периодическом издании Journal de mathematiques pures et appliquees работу, посвященную вращениям трехмерного пространства. Эта работа содержала практически полное описание алгебры кватернионов — Родригес назвал их параметрами группы вращений, — за исключением, пожалуй, самого слова «кватернион».
Забавно, что кватернионы Родригеса повторили судьбу его первого крупного открытия — формулы для полиномов Лежандра, которую Родригес вывел в своей диссертации De l'attraction des sphéroïdes. Эта формула, открытая им в 20 лет, была опубликована в 1816 году. Несмотря на это Джеймс Айвори и Карл Якоби «открыли» ее в 1824 и 1827 годах соответственно. Чтобы не обидеть никого из новых «первооткрывателей», формула получила название Айвори-Якоби. Только в 1878 году Эдуард Гейне указал на несправедливость, и формулу переименовали по фамилии первооткрывателя. Несмотря на это ее еще долго называли формулой Айвори-Якоби. Дальше, впрочем, все стало еще хуже: формулу Родригеса приняли за одно из определений полиномов Лежандра и вообще лишили наименования.
Но работа Родригеса, даже будучи опубликованной в довольно престижном математическом журнале, прошла незамеченной. Будто ее и не было. Возможно, она просто не попалась на глаза специалистам, возможно, математический труд известного банкира-социалиста априори воспринимался как блажь богача. А зря. Если бы на работу Родригеса внимание обратили вовремя, судьба как самих кватернионов, так и многих математиков могла бы сложиться гораздо менее драматично. Кто знает, может быть, сам Уильям Гамильтон не пал бы жертвой алкоголизма. Однако, обо всем по порядку.
Великий Гамильтон
Пока Родригес в перерывах между социалистическими диспутами занимался математикой, в Ирландии о совершенно другой задаче думал величайший математик своего времени Уильям Гамильтон. В 1833 году Гамильтон был первым (или одним из первых), кто понял, что известные к тому времени комплексные числа представляются в виде упорядоченных пар чисел действительных. Мы бы сейчас сказали, что Гамильтон догадался работать с двумерными векторами, но в то время и слова-то такого «вектор» математики еще не придумали.
Главное достоинство комплексных чисел заключается в том, что их можно не только складывать, но и умножать. Так вот, Гамильтон (как и многие математики его времени) задался вопросом: если можно умножать двойки чисел, то, быть может, можно умножать и тройки? Вопрос этот был важен по многим причинам, не последней из которых было то, что Гамильтон считал алгебру «наукой о чистейшем времени».
Гамильтон довольно долго (и бесплодно) занимался вопросом умножения троек. Даже дети математика, встречая его на лестнице каждое утро, задавали ему один и тот же вопрос: «Папа, ты уже научился умножать тройки чисел?» На это Гамильтон неизменно отвечал: «Нет, я пока могу их только складывать и вычитать».

Уильям Роуэн Гамильтон
Гамильтон был настоящим вундеркиндом. В 12 лет он знал 12 языков, в 17 лет самостоятельно нашел ошибку в «Небесной механике» Лапласа. В 18 лет написал первую серьезную работу по физике (геометрическая оптика). В 22, будучи еще студентом, стал Королевским астрономом Ирландии. В 30 был возведен в рыцарский титул. К 1843 году, когда Гамильтону было всего 38 лет, он уже был автором множества серьезных работ, в частности, сформулировал принципы гамильтоновой механики — формализма, лежащего в основе как классической, так и квантовой механики.
В понедельник 16 октября 1843 года (по некоторым данным, это было как раз в 49-й день рождения Бенжамена Родригеса) сэр Уильям Роуэн Гамильтон в сопровождении супруги прогуливался по Дублину в направлении Королевской академии. На подступах к Брумскому мосту, который Гамильтон во всех своих письмах почему-то упорно называл Брогемским, математика настигло озарение. Он понял, что надо работать не с тройками, а с четверками чисел. Легенда гласит, что в порыве вдохновения Гамильтон прямо на мосту (точнее на опоре моста у реки) накорябал знаменитое соотношение «i2 = j2 = k2 = ijk = -1». О том, как это восприняла супруга математика, умалчивается.
О своем открытии Гамильтон поспешил сообщить коллегам. Примечательно, что в своих сообщениях он снова назвал пресловутый мост Брогемским. Спустя несколько лет, когда история приобрела всемирную известность, власти Дублина переименовали мост. Так, по сути в один день, Уильям Гамильтон открыл кватернионы и переименовал мост.
Да, кстати, даже в названии своего детища Гамильтон не смог обойтись без пафоса (впрочем, на самого сэра Уильяма к тому времени давил уже по-настоящему тяжелый груз величия). По его собственному признанию (цитата приводится по книге Elements of Quaternions, 1901 год), слово «кватернион» родственно латинскому quaternio (то есть «четверка»), которое, в свою очередь, является синонимом греческого слова τετρακτύς. То есть кватернион — отражение того самого мистического тетрактиса пифагорейцев, который, как те считали, символизирует гармонию всех четырех сфер бытия и которому они приносили свою знаменитую клятву.
В общем, очевидно, что с открытием кватернионов Гамильтон связывал довольно большие надежды.
Задача Гамильтона
Итак, пришло время более точно сформулировать задачу, о которой думал Гамильтон.
Для начала напомним, что векторное пространство размерности n — это множество упорядоченных наборов из n действительных чисел. Нам потребуются пространства размерности не выше четвертой, поэтому мы будем иметь дело с двойками, тройками и четверками чисел. Векторы одной размерности можно складывать — достаточно просто сложить числа на соответствующих позициях. Векторы можно умножать на число — достаточно умножить на это число каждую компоненту набора. Векторами в физике обычно обозначают разного рода силы, скорости, ускорения и прочее. В общем, величины, имеющие помимо числового выражения еще и направление.

В отличие от обычных чисел, которые можно умножать, так просто придумать способ умножения (с хорошими свойствами) для векторов не получается. Например, если векторы умножать покомпонентно, как складывать, то произведение пар (1, 0) и (0, 1) будет давать (0, 0). Можно показать, что из-за этого ни у одного из множителей не будет обратного, то есть векторы с условием: его произведение с исходным дает единицу, то есть (1, 1). По сути, это означает, что в получившейся алгебре (векторное пространство с умножением называется алгеброй) нельзя делить на (1, 0). Или, если уж на то пошло, то на любой вектор (A, B), в котором одна из компонент равна нулю.
В некоторых случаях, однако, задача по нахождению способа умножения имеет решение. Например, если есть пары векторов (A, B) и (C, D), то их можно перемножить по формуле (AC - BD, AD + BC). Эта формула на первый взгляд кажется пугающей и неочевидной, однако она не что иное, как умножение комплексных чисел. Чтобы понять это, достаточно отождествить пару (A, B) с комплексным числом A + Bi, где i — та самая мнимая единица, число, в квадрате дающее минус 1, а также вызывающее ненависть и презрение у всех, кто мучился с математикой в школе. Современники Гамильтона полагали, что какая-нибудь хитрая формула должна быть и для умножения, например, троек. Именно ее искал Гамильтон.
Наши представления о векторах, которыми, как уже говорилось, математик не располагал, позволяют легко понять, что задача, которую он ставил перед собой, неразрешима. Для доказательства нам потребуется понятие базиса. Обозначим через 1, i, j тройки (1, 0, 0), (0, 1, 0) и (0, 0, 1) соответственно. Из правил сложения и умножения векторов немедленно вытекает, что тройку (A, B, C) можно представить в виде A 1 + B i + C j. Именно в таком виде и будем работать с элементами трехмерного пространства.

Брумский (Брогемский) мост
Фото: Wisher / Wikipedia
Какие свойства от гипотетического умножения, которое искал Гамильтон, можно потребовать? Во-первых, конечно, мы хотим, чтобы, по аналогии с комплексными числами, i, j были мнимыми единицами. То есть, i2 = j2 = - 1. При этом, конечно, единица должна вести себя как единица, то есть 1i = i1 = i, 1j = j1 = j. Кроме этого наше умножение, как и умножение обычное, должно подчиняться дистрибутивному и ассоциативному законам.
Теперь докажем, что мы хотим слишком многого.
Доказывать будем от противного. Рассмотрим произведение ij. Оно равно какому-то числу из нашего трехмерного пространства, то есть представляется в виде ij = A1 + Bi + C j. Умножим обе части равенства слева (на коммутативность мы не рассчитываем) на i. Учитывая i2 = - 1, получаем выражение - j = Ai - B1 + C ij. Подставим вместо ij исходное выражение и приведем подобные слагаемые. Получим выражение 0 = (CA - B) 1 + (CB + A) i + (C2 + 1) j. Равенство нулю означает, что нулю должны быть равны все компоненты тройки. Среди них, однако, имеется C2 + 1, который всегда больше нуля. Это противоречие завершает доказательство.
Коллеги мистического тетрактиса

Кегли для боулинга стоят в вершинах тетрактиса
Фото: Stefan Grazer / Wikipedia
Что же такого придумал Гамильтон, прогуливаясь с супругой? На самом деле гениальной догадку Гамильтона делают две вещи. Во-первых, он каким-то образом догадался, что надо рассматривать не тройки, а четверки чисел. Во-вторых, ему пришло в голову отказаться от коммутативности умножения.
Надо сказать, что второе было поистине революционным новаторством. Это сейчас, когда существует квантовая механика, некоммутативные объекты стали (условно) привычными — например, некоммутирующие линейные операторы, описывающие в квантовой механике положение и импульс системы (следствием именно некоммутативности является принцип неопределенности Гейзенберга), однако в середине XIX века люди о некоммутативных алгебрах не знали ничего.
Итак, кватернионами называются упорядоченные четверки действительных чисел (A, B, C, D). Действуя так же, как мы действовали выше, эти числа можно записывать выражением A1 + Bi + C j + D k. Соотношения между символами i, j, k ровно те, что написал на мосту Гамильтон, то есть i2 = j2 = k2 = ijk = - 1. Единица же (1) ведет себя так же, как единица в действительных числах.
Первые успехи и долгая дорога вниз
Научный мир встретил открытие Гамильтона с воодушевлением. Отец электромагнетизма и просто далеко не последний человек в физике Джеймс Клерк Максвелл писал: «Открытие кватернионного исчисления — это поистине скачок в нашем понимании свойств пространства, скачок, сравнимый, пожалуй, с открытием Декартом координатных троек!» Гамильтон же, провозгласив кватернионы своим величайшим открытием, принялся с воодушевлением (как он сам выражался) «расшифровывать послания высших сфер».
Сначала все шло довольно неплохо. Сначала Гамильтон придумал слово «вектор», которым мы так активно пользовались выше. Надо сказать, что векторы Гамильтона были вовсе не привычными нам векторами — так он назвал кватернионы, у которых первая компонента, то есть A, равна нулю (сейчас такие кватернионы принято называть чисто мнимыми). Так как чисто мнимые кватернионы образуют пространство размерности три, то великий Гамильтон решил, что его теория включает в себя всю механику — ведь, как говорилось выше, силы и другие физические величины записываются тройками чисел.

Джеймс Клерк Максвелл
Далее, записывая умножение кватернионов, он ввел две новые операции, каждая из которых сама по себе в будущем оказалась просто очень полезной: векторное и скалярное умножения. Сейчас эти операции известны даже школьнику, однако в середине XIX века они были настоящим откровением.
Однако дальше дело почему-то не пошло. Теория никак не хотела складываться. Но Гамильтона было не остановить — он с упорством искал своим кватернионам применение, которое никак не находилось. Разные историки оценивают этот поиск по-разному. Кто-то пишет, что это, мол, было похоже на бесплодные поиски единой теории всего, которыми занимался Эйнштейн. Кто-то говорит о настоящей одержимости, безумии (отягощенном неотвратимо наступающим алкоголизмом). Ситуация усугублялась тем, что вдруг выяснилось: в зачаточном состоянии кватернионы, оказывается, были еще у Гаусса, который просто не придал им значения и не стал публиковать полученные результаты. Гаусс изучал теорему о четырех квадратах — утверждение о том, что произведение двух чисел, представимых в виде суммы четырех квадратов, так же представляется в виде произведения четырех квадратов — прямое следствие кватернионного умножения.
После смерти Гамильтона все стало еще хуже. Приверженцы «кватернионного прогресса» становились все более и более похожими на агрессивную секту — их научные работы делались все более размытыми, менее математическими. Зато выпады в адрес оппонентов учения (а кватернионы довольно быстро перестали быть математической теорией, превратившись в набор, вообще говоря, неверных с точки зрения математики догм) становились острее. Вот, например, что писал любимый ученик Гамильтона Питер Тэт в ответ на выход книги «Векторный анализ» Гиббса: «Даже профессор Гиббс должен быть назван препятствием на пути кватернионного прогресса, ибо порожденный им памфлет "Векторный анализ" — это чудовище-гермафродит, объединивший в себе обрывки идей Гамильтона и Грассмана».
Нет ничего удивительного, что к концу века кватернионы стали восприниматься совсем неоднозначно. Лорд Кельвин в 1892 году писал про них так: «Кватернионы Гамильтона могут считаться чистейшим злом, которое не принесло ничего хорошего тем, кто работал с ними, включая, например, Клерка Максвелла». Несмотря на то, что после знаменитого «Рентгеновские лучи — это выдумка», к высказываниям лорда вообще следует относиться скептически, общее для того времени отношение к кватернионам он передал верно.
Наше время
Сейчас понятно, почему так случилось — Гамильтон очень серьезно просчитался, назвав векторами чисто мнимые кватернионы. Как показало появление тензорного анализа — основы основ всей физики, вектор от любого другого упорядоченного набора чисел отличается исключительно поведением при замене координат. Гамильтоновские векторы вели себя неправильно и, следовательно, не годились на роль тех самых физических наблюдаемых. Математически правильное описание кватернионов, а также их интерпретация были представлены в работе Родригеса, но о ее существовании, как говорилось выше, никто не знал. Да и прислушались бы великий Гамильтон и его ученики к утверждениям французского банкира-социалиста? Навряд ли.
Как бы то ни было, кватернионы заняли свое место в математике. В начале XX века были открыты спиноры — математические объекты, которые можно считать «правильным» обобщением векторов Гамильтона. Кроме этого, Фердинанд Фробениус доказал, что кватернионы — это, в некотором смысле, единственный способ продолжить умножение комплексных чисел на что-то большее с условием ассоциативности. Если отказаться от ассоциативности, то получатся так называемые числа Кэли, определяемые на восьмерках чисел.
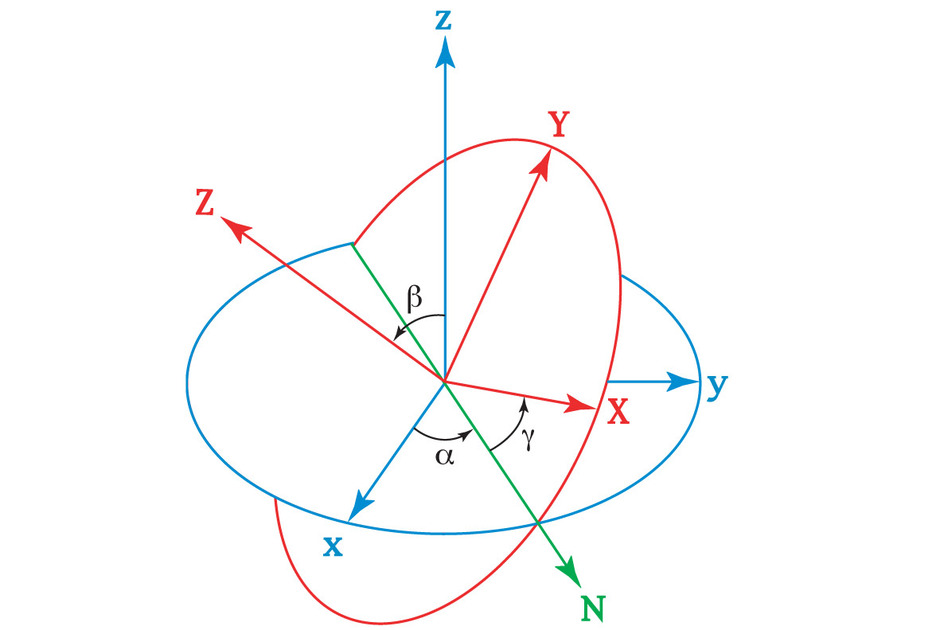
Углы Эйлера
Сейчас их активно используют, например, при компьютерном моделировании, а также в датчиках ориентации на самолетах. Кватернионный подход хорош тем, что, в отличие от так называемых углов Эйлера (их, например, любят астрономы), кватернионная интерпретация лишена особенностей, то есть таких точек, которые определяются несколькими значениями параметров одновременно. Из-за этого, в частности, основанные на кватернионах вычисления более устойчивы — то есть, грубо говоря, не сильно врут, если в начальных данных содержится небольшая ошибка. С другой стороны, у кватернионов нет такого, как у углов Эйлера, наглядного геометрического представления.
В общем, кватернионы — обычный себе математический объект. И не было бы у него такой богатой истории, если бы люди умели признавать ошибки. И этот вывод, в отличие от самих кватернионов, действительно можно назвать универсальным.