Нейробиологи из Великобритании провели эксперимент, в ходе которого попросили 15 математиков оценить красоту математических формул, предложив им список из 60 штук. После этого участникам эксперимента по очереди показывали красивые и некрасивые формулы. За откликом их мозга наблюдали при помощи функциональной магнитно-резонансной томографии (fMRI).
Как обнаружили нейробиологи, просмотр красивых, с точки зрения математиков, формул вызывает отклик в префронтальной коре головного мозга, отвечающей за сложные когнитивные функции и эмоции. Проанализировав отклик, ученые пришли к выводу, что восприятие красоты математики очень похоже на ощущение, возникающее во время прослушивания музыки или просмотра произведений живописи.
«Лента.ру» предлагает читателям самостоятельно оценить красоту некоторых математических формул, использовавшихся в этом эксперименте.
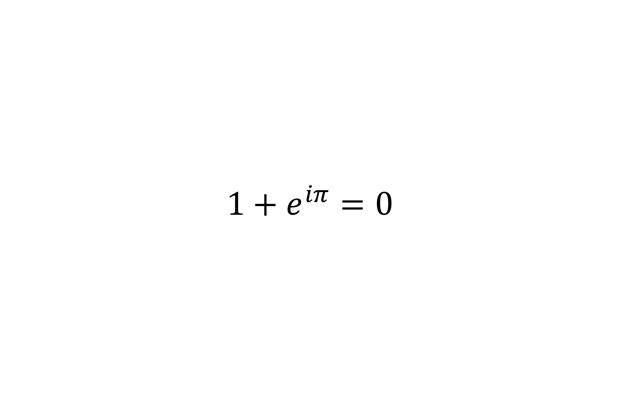
Тождество Эйлера
Тождество Эйлера является следствием формул Эйлера, связывающих экспоненту комплексного числа с тригонометрическими функциями. Эта формула является основной для экспоненциального представления комплексных чисел и формул Муавра для выражения синусов и косинусов кратных углов (в школе проходят частные случаи этой формулы для удвоенных и утроенных углов). Именно это тождество было признано участниками опыта самым красивым.
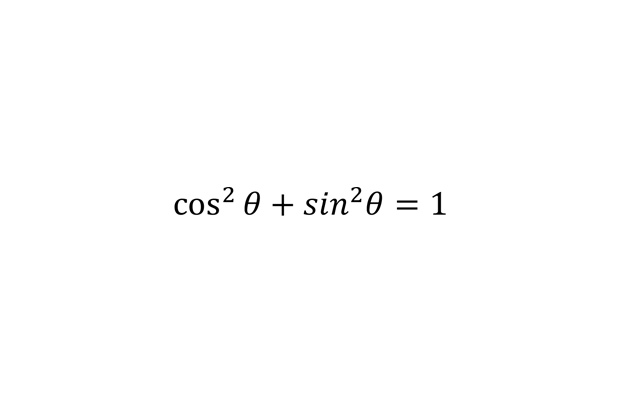
Основное тригонометрическое тождество
Эта формула связывает две основные тригонометрические функции. Обычно ее выводят геометрически, из теоремы Пифагора для прямоугольного треугольника с гипотенузой, равной единице: синус угла при гипотенузе будет в этом случае отношением противолежащего катета к гипотенузе, а косинус — прилежащего.
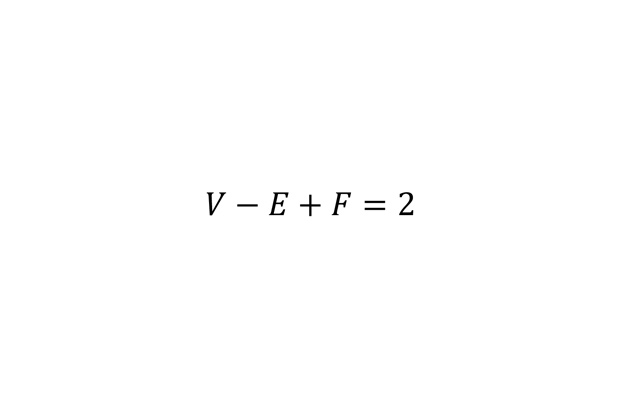
Формула для эйлеровой характеристики
В простейшем случае эта формула связывает между собой количество вершин (V), ребер (E) и граней (F) произвольного выпуклого многогранника.
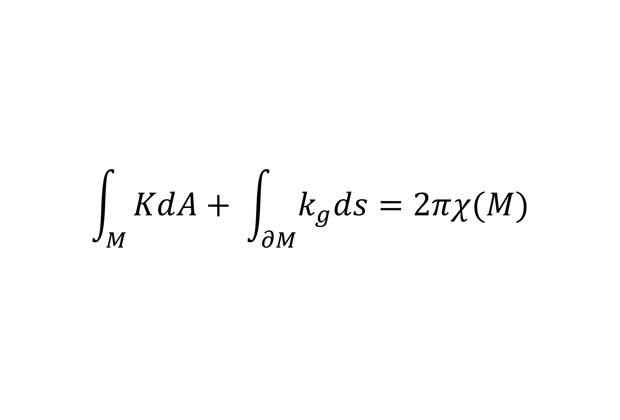
Формула Гаусса-Бонне
В частном случае эта формула связывает локальную характеристику поверхности под названием гауссова кривизна (она является мерой того, насколько поверхность отличается от плоскости) и ее глобальную, топологическую характеристику — количество сквозных дырок. Такая интерпретация подходит для двумерной поверхности, изготовленной из единого «куска» — например, сферы или тора. У сферы, кстати, сквозных дырок нет, а у тора она одна.
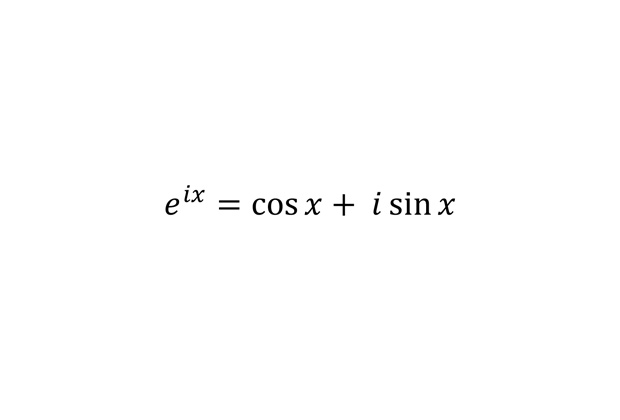
Формула Эйлера
Та самая формула Эйлера, о которой говорилось вначале. Тождество Эйлера является ее частным случаем, если вместо x подставить «пи».
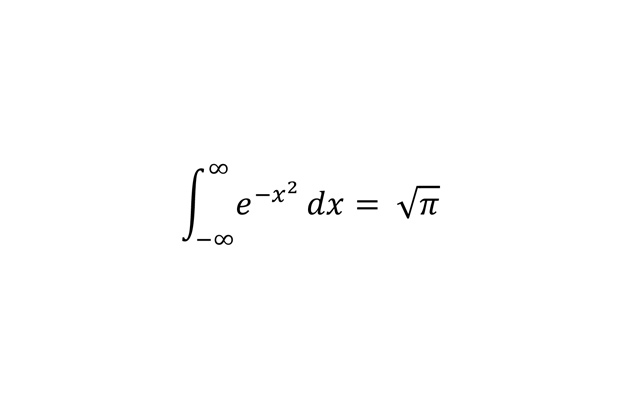
Гауссов интеграл (также известный как интеграл Эйлера-Пуассона)
Это выражение является инструментом для подсчета вероятностей в случае, когда речь идет о распределении Гаусса.
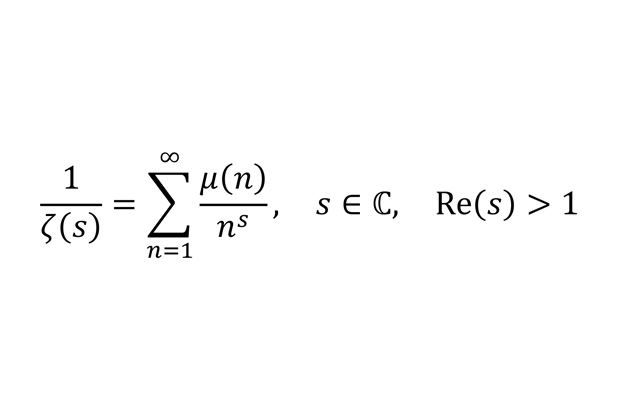
Формула Римана-Дирихле-Мёбиуса
В этой формуле слева стоит знаменитая дзета-функция Римана, а справа — ряд Дирихле для функции Мёбиуса. Функция Мёбиуса определена для натуральных чисел и возвращает 1, если число состоит из четного числа простых множителей, среди которых нет одинаковых, -1, если число состоит из нечетного числа таких множителей, и 0 — во всех остальных случаях. Эта формула демонстрирует глубокую связь дзета-функции с теорией чисел.
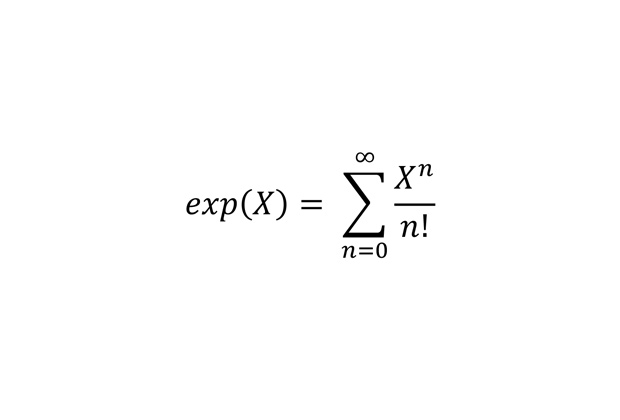
Формула для экспоненты
Представление экспоненты в виде ряда.
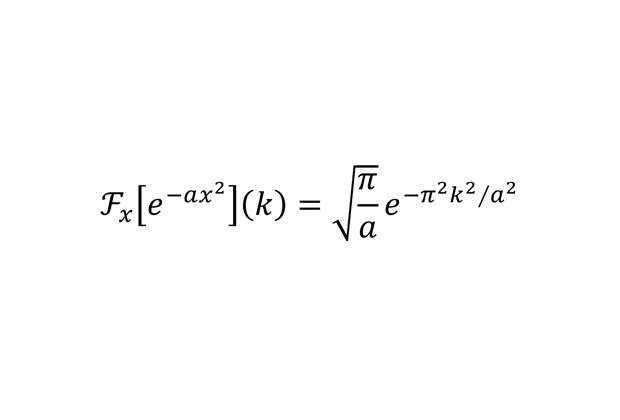
Преобразование Фурье от функции Гаусса
Эта формула показывает, что преобразование Фурье (используется, например, в радиотехнике, но далеко не только в ней) от гауссовой функции — это снова функция Гаусса, правда, с численным коэффициентом и другим множителем у показателя.
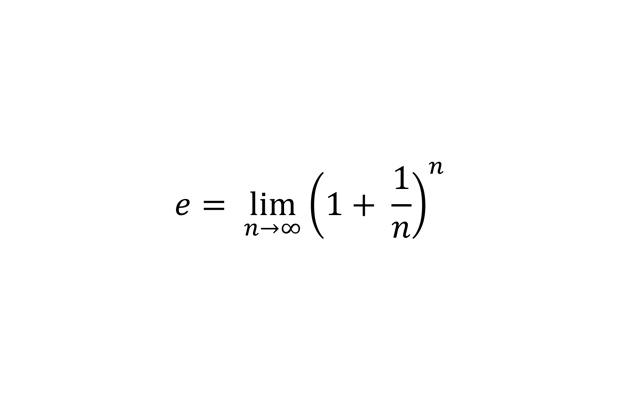
Число e
Определение числа e как предела некоторой числовой последовательности.
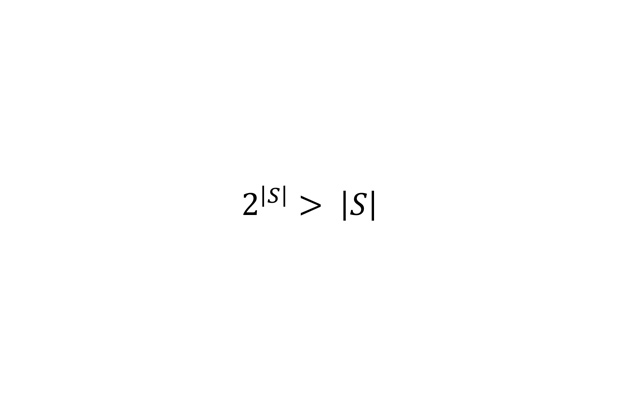
Теорема Кантора для натуральных чисел
Для сравнения двух бесконечных множеств в математике используется понятие биекции. Говорят, что два множества равномощны, если между их элементами можно установить взаимнооднозначное соответствие. Если, например, множество A равномощно некоторому подмножеству множества B, а B не равномощно A, то говорят, что B — мощнее. Теорема Кантора в данном случае утверждает, что множество точек отрезка мощнее множества натуральных чисел.
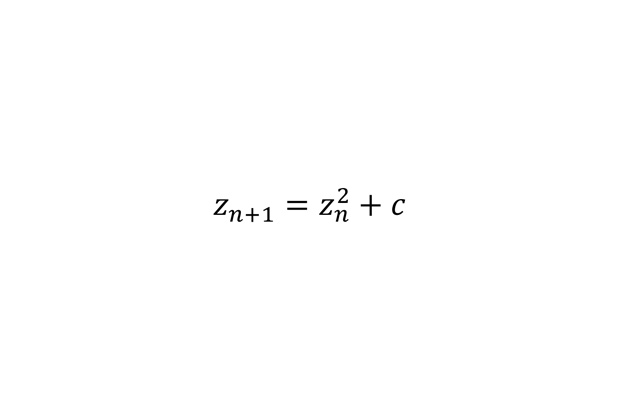
Квадратичный итерационный процесс
Бенуа Мандельброт обнаружил, что с помощью таких, казалось бы, простых процессов можно строить очень сложные множества. Он назвал их фракталами. Квадратичный итерационный процесс позволяет строить множество Мандельброта, названное в честь математика.
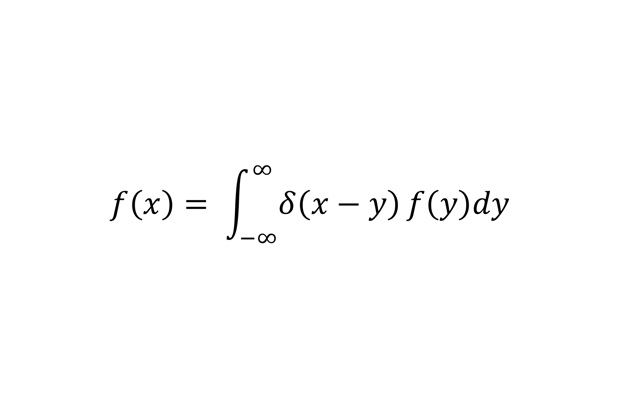
Дельта-функция Дирака
Дельта-функция является на самом деле не функцией, а обобщенной функцией. Приведенный интеграл можно использовать как ее определение. Такие функции очень активно используются в физике.
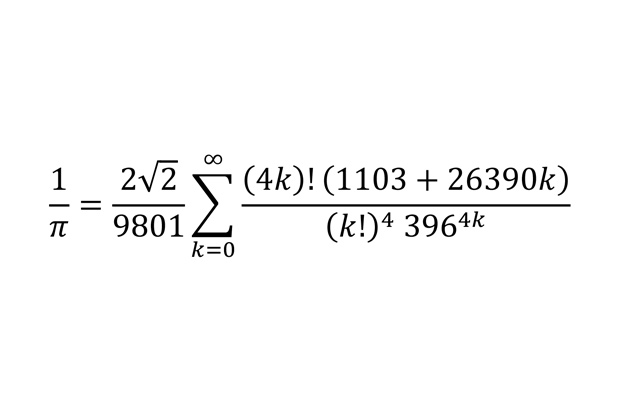
Формула Рамануджана
Эта формула для числа «пи» примечательна своей относительно быстрой (на момент открытия, конечно, то есть начала XX века) сходимостью ряда в правой части.
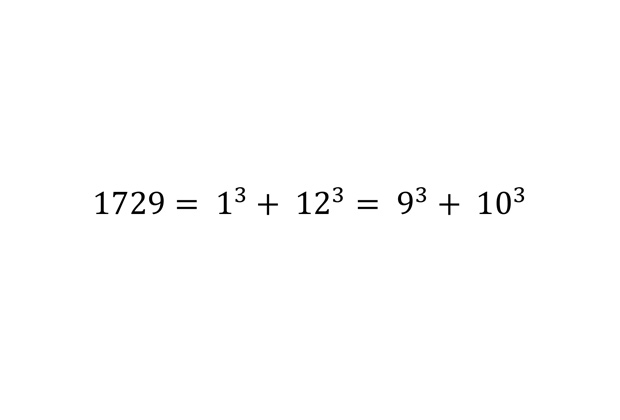
Минимальное число такси
Однажды математик Годфри Харди отправился навестить приболевшего математика Сриниваса Рамануджана. По прибытии Харди заметил, что приехал на такси «с достаточно скучным номером» 1729. На это Рамануджан немедленно возразил, что 1729 — очень интересное число. Это минимальное число из натуральных, для которого существует больше одного разложения в сумму двух кубов. Благодаря этой истории такие числа (то есть представимые в виде суммы двух кубов несколькими способами) получили наименования чисел такси.
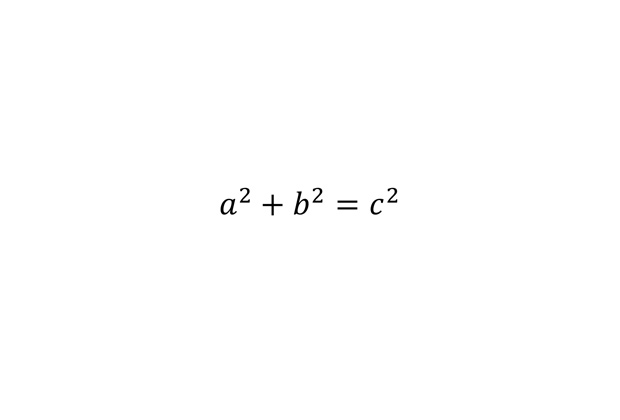
Теорема Пифагора
Сумма квадратов катетов равна квадрату гипотенузы. Эта теорема была известна еще в Междуречье примерно за 1800 лет до нашей эры.
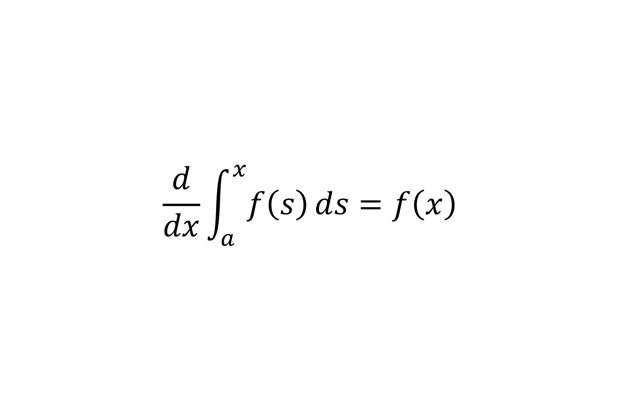
Первообразная и производная
Эта формула является частным случаем формулы Ньютона-Лейбница. Она позволяет связать две важнейшие операции математического анализа — дифференцирование и интегрирование.
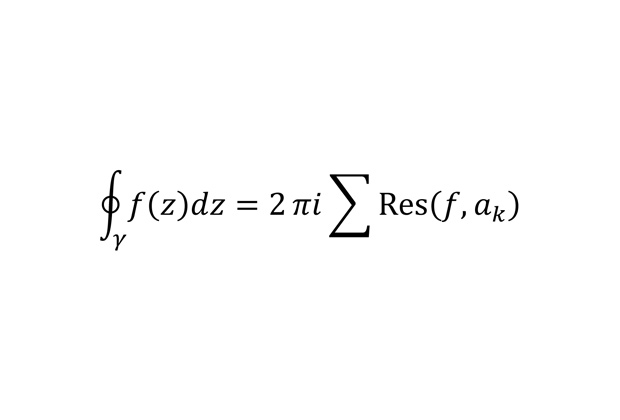
Теорема Коши о вычетах
Теорема утверждает, что, когда речь идет о комплексных функциях, для подсчета интеграла по замкнутому контуру достаточно вычислить некоторые величины в особых точках функции, именуемые вычетами, которые попали в ограниченную контуром область. Благодаря этой теореме, например, становится возможным подсчет разных бесконечных сумм.
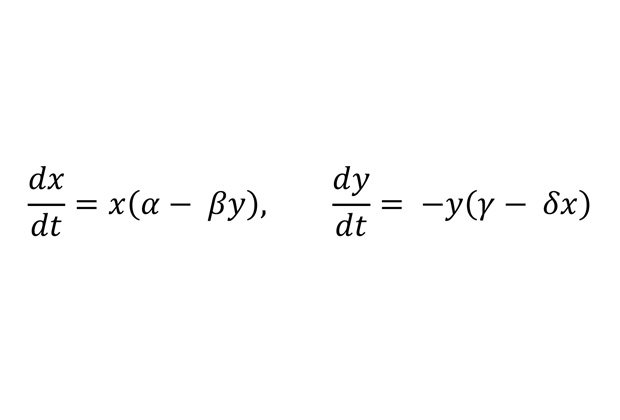
Модель Лотки-Вольтерры
Эта система нелинейных дифференциальных уравнений описывает динамику в простейшей экосистеме, состоящей из одного вида хищников и одного вида жертв. Часто используется как пример сравнительной неустойчивости равновесия в таких экосистемах — достаточно сильное возмущение может приводить к вымиранию видов.
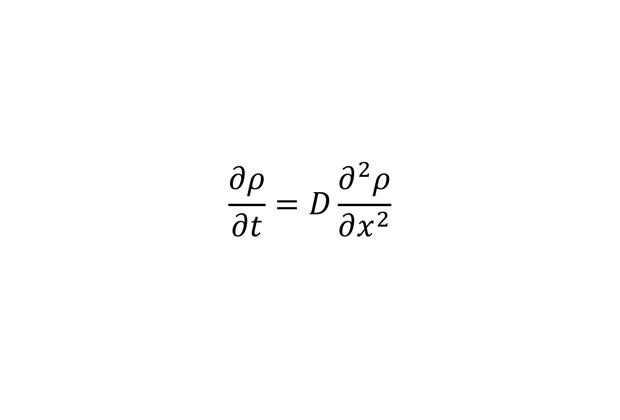
Уравнение диффузии
Уравнение описывает процесс диффузии — то есть постепенного взаимного проникновения — двух сред.
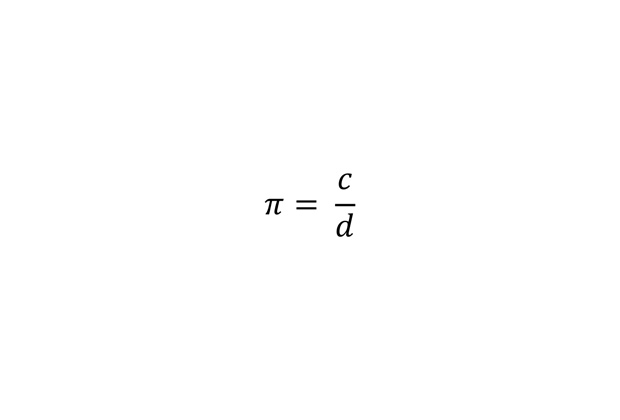
Формула для «пи»
Пожалуй, самая главная формула для числа «пи». Здесь c — длина окружности, а d — ее диаметр.
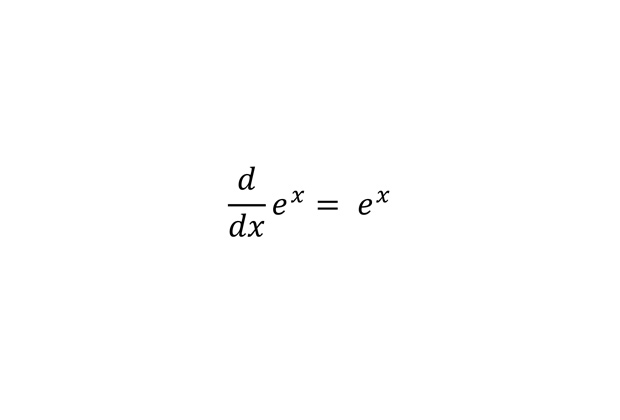
Дифференцирование экспоненты
Одно из замечательнейших свойств экспоненты: ее производная равна ей самой. Легко показать, что экспонента — единственная с точностью до умножения на константу функция, обладающая таким свойством.
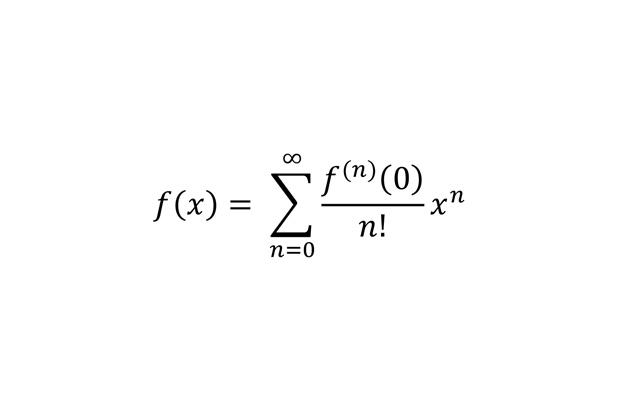
Ряд Тейлора-Маклорена
Представление аналитической функции в виде ряда в нуле. Вообще говоря, такой ряд можно построить для более широкого класса функций, называемых гладкими, однако в этом случае в формуле нельзя ставить знак равенства.
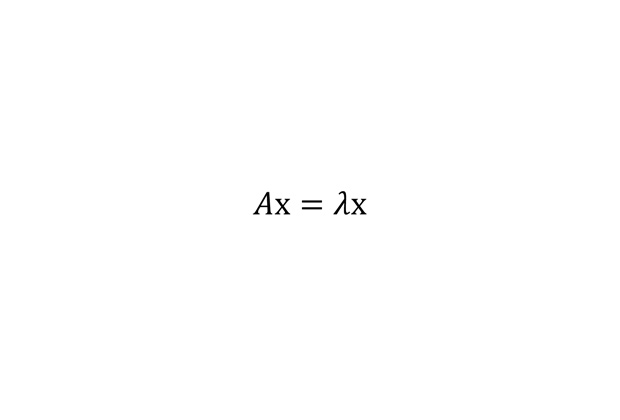
Уравнение для собственного вектора оператора
Понятие собственного вектора оператора, то есть вектора, который при действии этого оператора просто растягивается, является одним из ключевых в линейной алгебре. Это понятие крайне полезно, например, в квантовой механике — состояния квантовых систем есть собственные вектора в некотором (правда, бесконечномерном) пространстве.
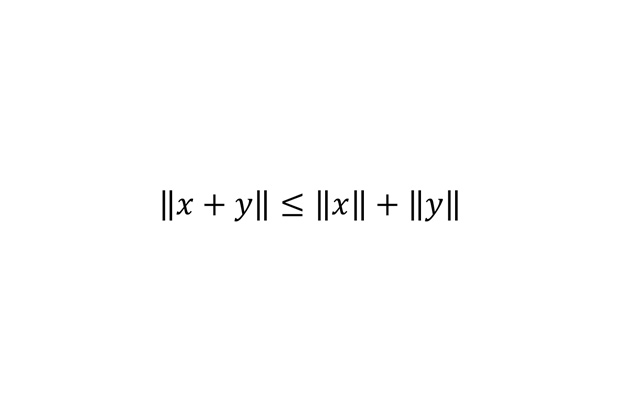
Неравенство треугольника
Неравенство треугольника для нормированных пространств. Простейший пример такой нормы — это корень квадратный из суммы квадратов координат вектора в трехмерном пространстве. В этом случае это неравенство превращается в обычное неравенство треугольника: сумма двух сторон не меньше третьей.
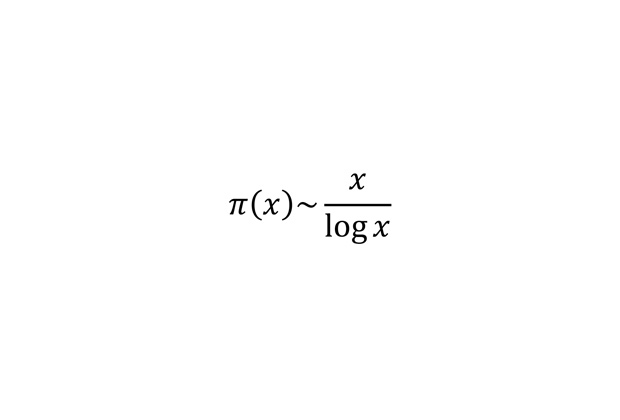
Асимптотика пи-функции
Пи-функцией называется функция, которая возвращает количество простых чисел меньше данного действительного x или равных ему. Как показал в XIX веке Жак Адамар, эта функция растет примерно как отношение в правой части. Это означает, что простых чисел, не превосходящих x, примерно x/log x.
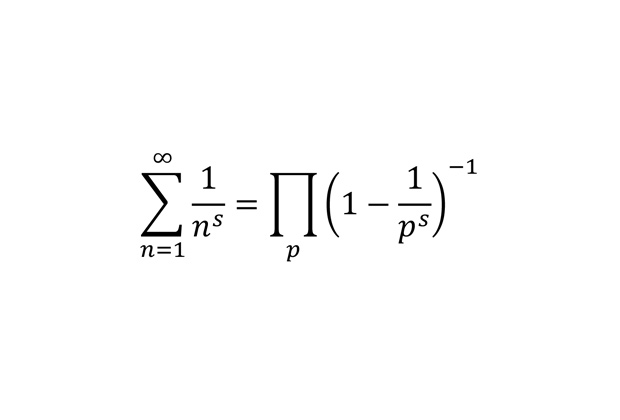
Формула Эйлера для дзета-функции Римана
Как оказалось, иногда бывает полезно работать не с бесконечными суммами, а с бесконечными произведениями. В правой части стоит произведение по всем простым числам p — еще один замечательный факт, связывающий дзета-функцию и теорию чисел.
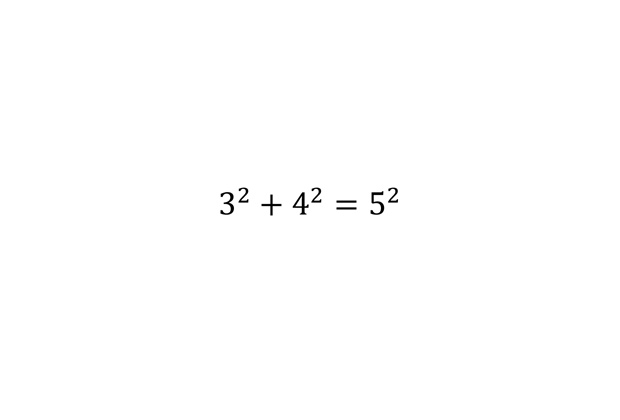
Пифагорова тройка
Тройки натуральных чисел, которые могут быть сторонами прямоугольного треугольника, получили название пифагоровых. Считается, что тройка (3, 4, 5) была известна еще древним египтянам.
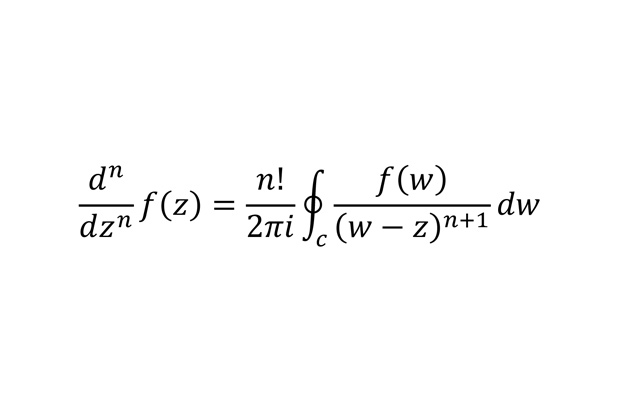
Интегральная формула Коши
Формула позволяет связать кратные производные комплексно-аналитической функции с интегралом по контуру. Благодаря этой формуле доказывается эквивалентность нескольких определений комплексно-аналитической функции. В частности, если она дифференцируема, то немедленно раскладывается в сходящийся ряд.
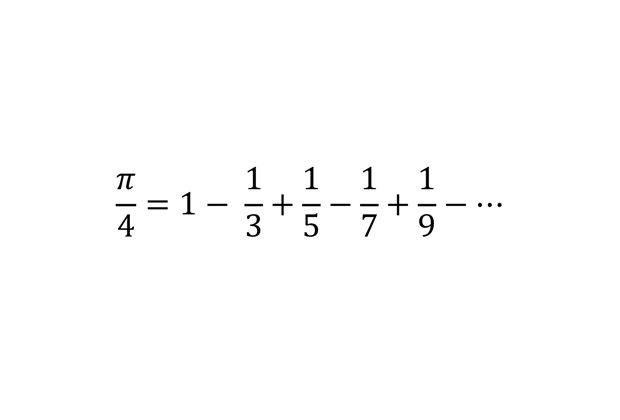
Число «пи» в виде ряда
Представление числа «пи» в виде ряда от дробей с нечетными знаменателями.
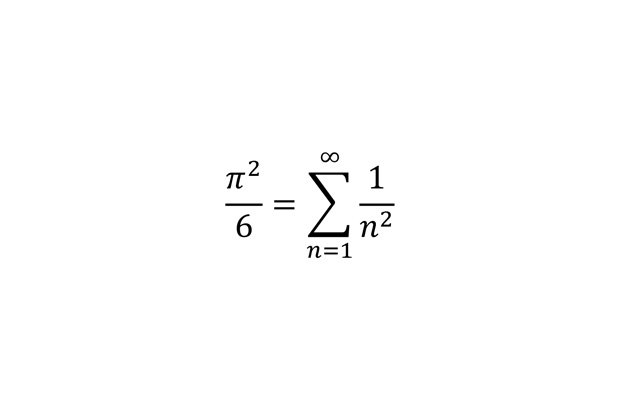
Эйлерова сумма обратных квадратов
В возрасте 28 лет Леонард Эйлер доказал, что сумма обратных квадратов связана с числом «пи». Это немедленно принесло ему славу — на тот момент задача о суммировании считалась крайне сложной, над ней безуспешно бились лучшие умы того времени.
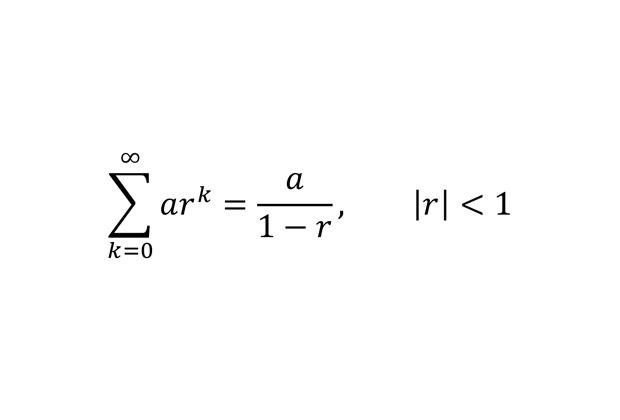
Сумма геометрической прогрессии
Геометрической прогрессией называется последовательность чисел, в которой каждое следующее получается из предыдущего умножением на некоторое фиксированное число r.
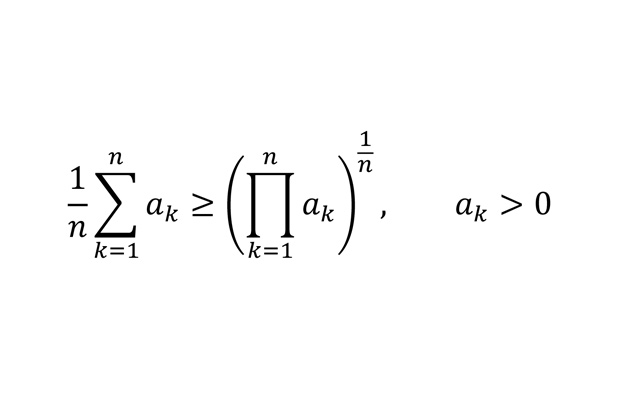
Неравенство для средних, открытое Коши
Неравенство связывает среднее арифметическое и среднее геометрическое чисел.
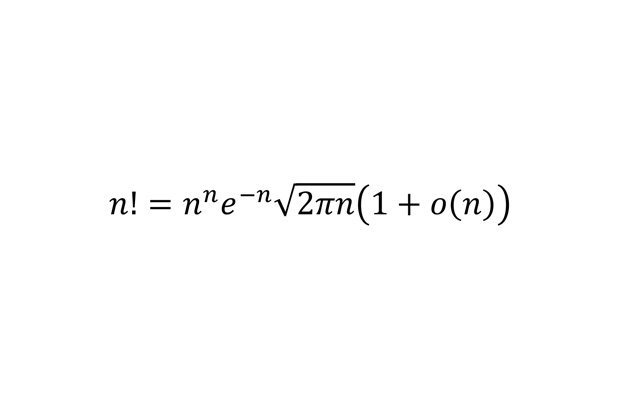
Формула Стирлинга
Формула Стирлинга позволяет оценить скорость роста такой функции, как факториал n!
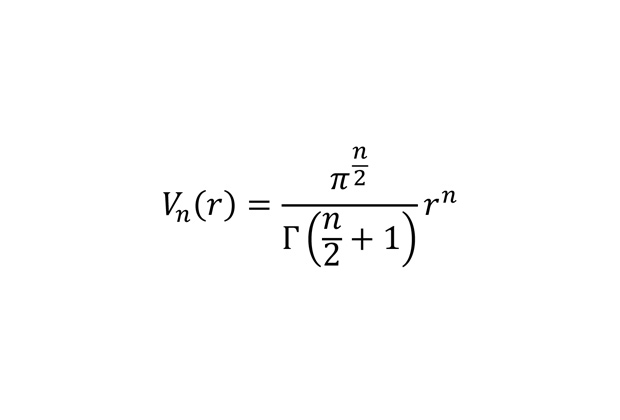
Объем n-мерного шара радиусом r
В формулу для объема n-мерного шара входит гамма-функция.
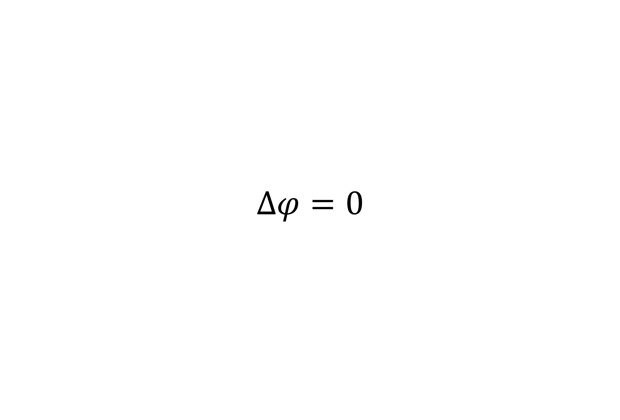
Уравнение Лапласа
Это уравнение возникает в задачах механики, теплопроводности, электростатики, гидравлики. Оператор Лапласа, стоящий в левой части, играет важную роль в квантовой механике. Там с его помощью определяется уравнение Шрёдингера.
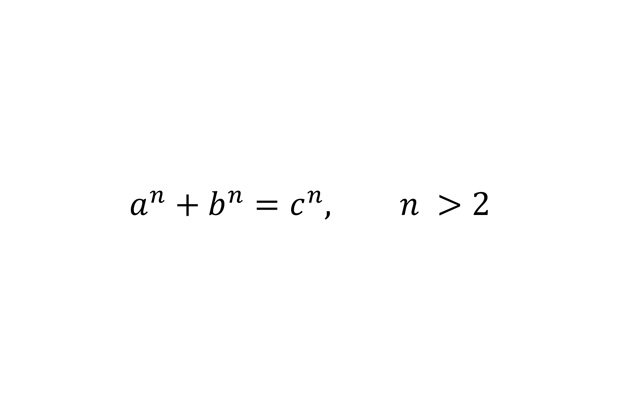
Великая теорема Ферма
Утверждение великой теоремы Ферма, доказанной в 1995 году Эндрю Уайлзом, говорит, что записанное уравнение не разрешимо для целых ненулевых a, b, c.
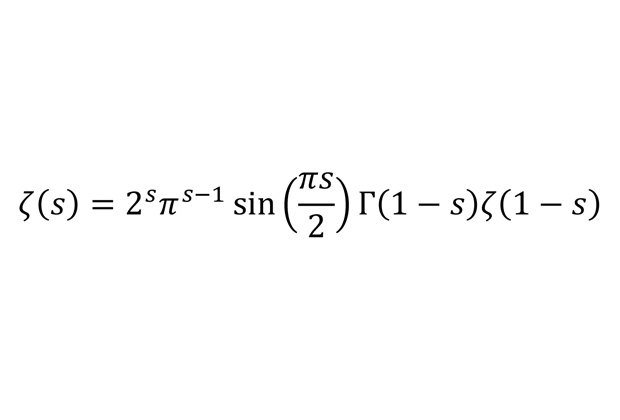
Функциональное уравнение на гамма- и дзета-функции
Это уравнение позволяет, среди прочего, формализовать понятие «суммы всех натуральных чисел», которое возникает в теории струн.